Understanding probability theory can be a daunting task, especially when dealing with terms like disjoint events. So, what are disjoint events exactly? Disjoint events, also known as mutually exclusive events, refer to events that cannot occur simultaneously. In simpler terms, if one event happens, the other event cannot occur at the same time. This concept plays a crucial role in calculating probabilities, as the occurrence of one event affects the likelihood of the other event happening. In this blog, we will delve deeper into the definition of disjoint events, explore examples to clarify the concept, and discuss how they impact probability calculations. Let’s unravel the mysteries behind disjoint events together!
Introduction to Disjoint Events
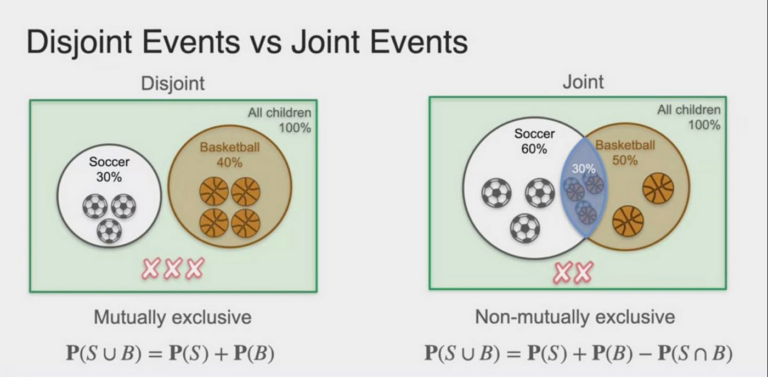
Understanding disjoint events is essential in probability theory. Disjoint events, also known as mutually exclusive events, are events that cannot occur simultaneously. This means that if one event happens, the other cannot. In simpler terms, the occurrence of one event prevents the other from occurring. Disjoint events have a probability of 0 when considered together.
Key Characteristics of Disjoint Events
Disjoint events have the following key characteristics:
- They do not have any outcomes in common.
- When one event happens, the other event cannot occur at the same time.
- The probability of the union of disjoint events is the sum of the probabilities of the individual events.
Example Scenario of Disjoint Events
Imagine a standard deck of playing cards. Drawing a red card and drawing a black card are disjoint events since a card cannot be both red and black at the same time. If we define event A as drawing a red card and event B as drawing a black card, then P(A and B) = 0.

Understanding Disjoint Events
Disjoint events, also known as mutually exclusive events, are events that cannot occur simultaneously. In simpler terms, if one event happens, the other event cannot occur at the same time. Understanding disjoint events is crucial in probability theory as it helps in calculating the likelihood of different outcomes.
Characteristics of Disjoint Events
Disjoint events have the following key characteristics:
- They have no outcomes in common.
- If event A occurs, event B cannot occur, and vice versa.
- The probability of the union of disjoint events is the sum of the individual probabilities.
Example of Disjoint Events
Consider tossing a coin. The events of getting a heads and getting a tails are disjoint events because both events cannot happen simultaneously in a single toss. If you get heads, you cannot get tails at the same time and vice versa.

Examples of Disjoint Events
Disjoint events, also known as mutually exclusive events, are events that cannot occur simultaneously. When one event happens, the other event cannot occur at the same time. Understanding examples of disjoint events is crucial in probability theory and statistics.
Rainy Day or Sunny Day
Consider the events of having a rainy day and a sunny day in a particular location. These events are disjoint as both cannot happen simultaneously. If it is raining, it cannot be sunny at the same time.
Head or Tail in Coin Toss
Another example of disjoint events is flipping a coin and getting either a head or a tail. Heads and tails are mutually exclusive outcomes in a coin toss.
Image: Example of Disjoint Events in a Venn Diagram

Intersection of Disjoint Events
When discussing the concept of disjoint events, it is crucial to understand the notion of their intersection. Disjoint events, also known as mutually exclusive events, refer to events that cannot occur simultaneously. Therefore, their intersection is always an empty set, denoted as ∅. This means that if Event A and Event B are disjoint, the probability of both events occurring together is zero.
Example of Intersection of Disjoint Events
For instance, consider rolling a six-sided die. Events “rolling an even number” and “rolling an odd number” are disjoint since a number cannot be both even and odd simultaneously. As a result, their intersection is empty, yielding a probability of zero for rolling both an even and an odd number on the same roll.
Applications in Probability Theory
The concept of the intersection of disjoint events is fundamental in probability theory. It helps in determining the probabilities of compound events and understanding the relationship between different outcomes. By recognizing when events are disjoint, one can easily calculate the overall probability of a set of events occurring.
Calculating Probability with Disjoint Events
When it comes to understanding probability in the context of disjoint events, it is essential to grasp the concept of events that cannot occur simultaneously. Disjoint events, also known as mutually exclusive events, refer to events that have no outcomes in common. These events do not overlap and are considered independent of each other.
Probability of Disjoint Events
Calculating the probability of disjoint events involves simple arithmetic. To find the likelihood of either event occurring, you can add their individual probabilities. Mathematically, if A and B are disjoint events, then P(A or B) = P(A) + P(B). This formula holds true when dealing with mutually exclusive events.
For example, if the probability of event A happening is 0.4 and the probability of event B occurring is 0.6, the probability of either A or B occurring would be 0.4 + 0.6 = 1.
Calculating Probability with Real-World Scenarios
Applying the concept of disjoint events to real-world scenarios can help in making informed decisions. Consider a scenario where you are calculating the probability of drawing a red card or a black card from a deck of cards. Since a card cannot be both red and black simultaneously, these events are disjoint.
- Red Cards: Probability = Number of Red Cards / Total Number of Cards
- Black Cards: Probability = Number of Black Cards / Total Number of Cards
Frequently Asked Questions
-
- What are disjoint events?
- Disjoint events, also known as mutually exclusive events, are events that cannot happen at the same time. If one event occurs, the other event cannot occur simultaneously.
-
- How do disjoint events impact probability?
- In probability theory, when two events are disjoint, the probability of either event occurring is the sum of the probabilities of each individual event. This is because the events do not overlap, so the probability of their union is simply the sum of their individual probabilities.
-
- Can disjoint events be independent?
- Disjoint events are not independent because the occurrence of one event implies that the other event cannot occur. Independence between events means that the occurrence of one event does not affect the probability of the other event happening.
-
- What is an example of disjoint events?
- An example of disjoint events is rolling a die and getting a 1, or rolling a die and getting an even number. These events are mutually exclusive because you cannot roll a 1 and an even number at the same time.
Final Thoughts
Understanding what disjoint events are is crucial in the world of probability. In essence, disjoint events are events that cannot occur simultaneously. By grasping this concept, we can better calculate probabilities and make informed decisions. Disjoint events play a significant role in various fields such as statistics, finance, and even everyday scenarios. By recognizing the impact of disjoint events on probability, we can enhance our problem-solving skills and approach situations with a logical mindset. Remember, when events are disjoint, the probabilities add up. So, next time you encounter disjoint events, embrace the opportunity to apply your newfound knowledge and unravel the mysteries of probability with confidence!