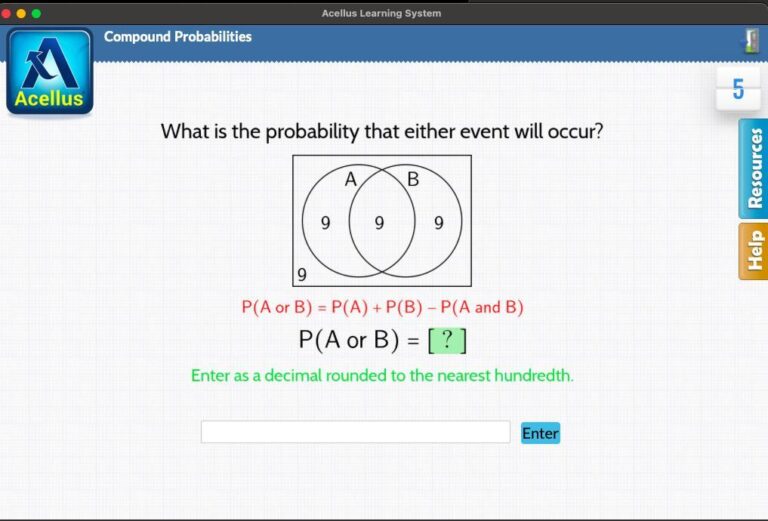
Have you ever pondered over the probability of either event occurring in a given scenario? Understanding the likelihood of outcomes is a crucial aspect of decision-making and risk assessment. In our exploration today, we delve into the captivating world of probabilities and odds. What is the probability that either event will occur? This question forms the crux of our discussion, guiding us through the realms of uncertainty and chance. Join us as we navigate through the intricacies of probability theory, scenarios where multiple events can happen, and how to calculate the chances of their occurrence. Let’s unlock the mysteries behind the numbers and learn to interpret the odds effectively.
Introduction to Probability
Understanding probability is crucial in making informed decisions in various aspects of life. Probability refers to the likelihood of an event occurring and is expressed as a number between 0 and 1. A probability of 0 indicates that the event will not occur, while a probability of 1 signifies that the event is certain to occur. When we consider the question, “What is the probability that either event will occur?”, we delve into the realm of analyzing and quantifying uncertainty.
The Basics of Probability
Probability theory involves the study of random events and the likelihood of their outcomes. It is based on the concept of a sample space, which consists of all possible outcomes of an experiment. Events within this sample space are subsets that represent specific outcomes or sets of outcomes. Calculating probabilities involves determining the ratio of favorable outcomes to the total possible outcomes.
Types of Probability Events
There are different classifications of probabilities, including marginal probability, conditional probability, and joint probability. Marginal probability focuses on the likelihood of a single event occurring independently. Conditional probability considers the probability of an event given that another event has already occurred. Joint probability, on the other hand, deals with the likelihood of two or more events occurring simultaneously.
Defining Events and Outcomes
When we talk about what is the probability that either event will occur, it’s essential to understand the concept of defining events and outcomes. In the realm of probability, an event is a set of outcomes or a possible result of an experiment. On the other hand, outcomes are the possible results of an experiment, event, or situation.
Understanding Events
An event can be a single outcome or a combination of outcomes. It could be as simple as rolling a dice and getting a specific number, or as complex as drawing two cards from a deck and getting a pair.
Events are typically denoted by letters such as A, B, or C, and they can be classified as simple events (single outcomes) or compound events (combinations of outcomes).
Outcomes and Sample Space
The set of all possible outcomes of an experiment is known as the sample space. Each outcome within the sample space is unique and collectively covers all possible results of the experiment.
For example, when flipping a coin, the sample space consists of two outcomes: heads and tails. This forms the basis for calculating probabilities and determining the likelihood of different events.
Calculating the Probability of Individual Events
When determining the probability of individual events, it is crucial to consider the number of possible outcomes favorable to the event and divide it by the total number of outcomes. This calculation provides the likelihood of the specific event occurring.
Understanding Probability Calculation
To calculate the probability, you need to divide the number of favorable outcomes by the total number of outcomes. For example, if there are 3 favorable outcomes out of 10 total outcomes, the probability would be 3/10 = 0.3.
Example of Probability Calculation
Suppose you are rolling a fair six-sided die. The probability of rolling a 3 would be 1/6, as there is only one favorable outcome (rolling a 3) out of six possible outcomes (numbers 1 to 6).

Understanding the Union of Events
When considering the probability of either event occurring, it is vital to understand the concept of the union of events. The union of two events A and B, denoted by A ∪ B, represents the outcome where either event A or event B or both occur. In simpler terms, it combines the possibilities of both events happening into one collective outcome.
Calculating the Probability of Union of Events
To determine the probability of the union of two events, you must consider the individual probabilities of each event and the intersection of the two events. The formula for the union of events A and B is given by:
P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
Real-World Example: Tossing a Coin and Rolling a Die
Consider the scenario where you toss a coin and roll a six-sided die. Let event A be getting a head on the coin, and event B be rolling a prime number on the die. The probability of either event A or event B occurring can be calculated using the above formula.
Let’s illustrate this scenario:
- Probability of event A (getting a head) = 1/2
- Probability of event B (rolling a prime number) = 3/6 = 1/2
- Probability of both events happening (A ∩ B) = 1/2 * 1/6 = 1/12
- Substitute these values in the formula to find P(A ∪ B).

Calculating the Probability of Either Event Occurring
Calculating the probability of either event occurring involves understanding the likelihood of one event, the other event, or both events happening. To determine this probability, we can use the formula:
Probability of Event A or B = P(A) + P(B) – P(A and B)
Understanding the Formula
The probability of either event A or event B occurring is calculated by adding the individual probabilities of each event and subtracting the probability of both events occurring simultaneously. This adjustment ensures that the double-counted overlap is accounted for.
For example, if the probability of event A is 0.6 and the probability of event B is 0.4, and the probability of both events happening together is 0.2, the probability of either event A or event B occurring is:
0.6 + 0.4 – 0.2 = 0.8
Application in Real-Life Scenarios
In real-life scenarios such as predicting the likelihood of rain or sunshine, calculating the probability of either event occurring helps in decision-making processes. Understanding the combined chances of different outcomes can assist in risk assessment and strategic planning.
Real-life Applications of Probability
Probability plays a crucial role in various real-life applications, providing insights into uncertain events and helping in decision-making processes. Let’s explore some practical examples of how probability is utilized:
Weather Forecasting
Weather forecasting heavily relies on probability to predict future weather patterns. Meteorologists analyze historical data and current atmospheric conditions to calculate the likelihood of different weather events occurring, such as rain, snow, or sunny weather in a particular year.
Medical Diagnosis
Probability is used in medical diagnosis to assess the likelihood of a patient having a particular disease based on symptoms, test results, and risk factors. Doctors apply statistical models to make informed decisions about treatment options for patients.
Sports Analytics
In sports, probability helps in predicting match outcomes, player performance, and game strategies. Sports analysts use probability models to calculate win probabilities, player statistics, and optimize team tactics for competitive advantage in the game.
Financial Risk Management
Financial institutions use probability to assess and manage various risks, such as market fluctuations, investment outcomes, and loan defaults. By understanding the probabilities of different scenarios, organizations can make informed decisions on their investments.
Frequently Asked Questions
-
- What does it mean for events to occur?
- Events occur when a particular outcome or result happens.
-
- What is the probability of an event occurring?
- Probability is a measure of the likelihood that an event will happen, expressed as a number between 0 and 1.
-
- What is the concept of ‘either/or’ events in probability?
- In probability, ‘either/or’ events refer to situations where there are two possible outcomes, and we are interested in the probability of at least one of them happening.
-
- How do you calculate the probability that either event will occur?
- To calculate the probability that either event will occur, you can use the formula P(A or B) = P(A) + P(B) – P(A and B), where P(A) and P(B) are the individual probabilities of each event, and P(A and B) is the probability that both events happen at the same time.
-
- Can the probability of either event occurring be greater than 1?
- No, the probability of either event occurring cannot be greater than 1, as probability values range from 0 to 1.
-
- Why is understanding the probability of either event occurring important?
- Understanding the probability of either event occurring is important in decision-making, risk assessment, and many real-world applications where knowing the likelihood of certain outcomes is crucial.
Final Thoughts
Understanding the probability that either event will occur is essential in making informed decisions, whether in gambling, business, or everyday life. By exploring the odds associated with different outcomes, we gain valuable insights into the likelihood of specific events taking place.
Through this blog, we have delved into the concept of probability, calculating the chances of either event occurring, and interpreting the results. Remember, probability is not just about luck; it involves a systematic approach to evaluating uncertainties.
By grasping the fundamentals of probability, we equip ourselves with the tools to assess risks, make sound judgments, and anticipate outcomes. So next time you face a decision or a gamble, remember to consider the probability that either event will occur.