Unraveling the Mysteries of Disjoint Events: What You Need to Know

Have you ever come across the term “disjoint events” and found yourself puzzled by its meaning? Fear not, for this blog is here to shed light on this concept and equip you with a better understanding of it. Disjoint events, also known as mutually exclusive events, are fundamental in the realm of probability theory and statistics. In simple terms, disjoint events are events that cannot occur simultaneously. Understanding the characteristics and implications of disjoint events is crucial for making informed decisions in various fields, from finance to science.

Disjoint events in probability theory are events that cannot occur simultaneously. In simpler terms, if one event takes place, the other event cannot happen at the same time. Understanding the concept of disjoint events is crucial in probability and statistics to determine the likelihood of different outcomes.

Key Characteristics of Disjoint Events

Disjoint events are also known as mutually exclusive events. These events have no outcomes in common and do not intersect. When calculating the probability of disjoint events, you add the individual probabilities of each event. For instance, if event A and event B are disjoint, then P(A or B) = P(A) + P(B).

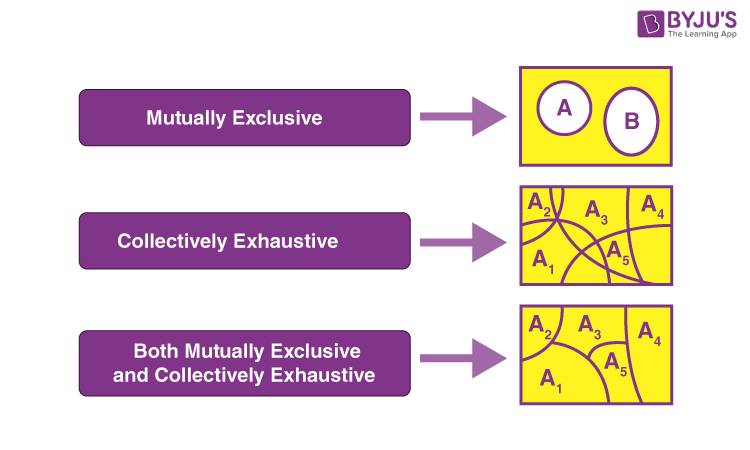
Disjoint events can be illustrated using Venn diagrams, where separate circles represent each event, and there is no overlap between them.

Example of Disjoint Events

Imagine tossing a fair six-sided die. Event A is getting an odd number (1, 3, or 5), and event B is getting an even number (2, 4, or 6). These events are disjoint because a single outcome cannot be both odd and even. The probability of landing on an odd number (P(A)) is 3/6 or 0.5, and the probability of landing on an even number (P(B)) is also 3/6 or 0.5.

In this scenario, given that A and B are disjoint events, P(A or B) = P(A) + P(B) = 0.5 + 0.5 = 1.

Understanding the concept of disjoint events is crucial in probability theory as it helps in analyzing the probability of multiple events occurring simultaneously. Disjoint events, also known as mutually exclusive events, refer to events that cannot occur at the same time. This leads to a fundamental property where the occurrence of one event prevents the occurrence of the other event. This exclusion principle plays a significant role in various statistical analyses and decision-making processes.

The Significance in Probability Calculations

Disjoint events are essential in calculating the total probability of all possible outcomes in a given sample space. By identifying and understanding disjoint events, it becomes easier to compute the chances of specific outcomes or combinations. This information is invaluable in fields such as finance, insurance, and risk management where accurate probability assessments are critical for decision-making.

Application in Real-World Scenarios

In real-world scenarios, recognizing disjoint events helps in simplifying complex situations into manageable probabilities. For example, in a game of rolling a standard six-sided dice, getting either a 2 or a 4 are disjoint events since they cannot happen simultaneously. This simplification aids in making informed choices based on calculated risks and potential outcomes.

When delving into the realm of probability and statistics, understanding disjoint events is crucial. Disjoint events, also known as mutually exclusive events, are events that cannot occur simultaneously. In simpler terms, if one event takes place, the other event cannot happen at the same time. Let’s explore some real-world examples to grasp this concept better:

Example 1: Tossing a Coin

One classic example of disjoint events is tossing a fair coin. The outcomes “landing on heads” and “landing on tails” are mutually exclusive. If the coin lands on heads, it cannot land on tails simultaneously. This makes these events disjoint, as only one outcome can occur in a single toss.

Example 2: Rolling a Die

Consider rolling a standard six-sided die. The events “rolling an odd number” and “rolling an even number” are disjoint events. It is impossible for the die to show both an odd and an even number simultaneously. Thus, these outcomes are mutually exclusive in a single roll of the die.

Understanding the probability of disjoint events is crucial in the realm of statistics and probability theory. Disjoint events, also known as mutually exclusive events, are events that cannot occur simultaneously. In simpler terms, if one event happens, the other event cannot occur at the same time. This concept plays a fundamental role in calculating probabilities and making informed decisions based on the outcomes.

Importance of Disjoint Events

Disjoint events are essential in probability theory as they help in determining the likelihood of specific outcomes in various scenarios. By understanding the concept of disjoint events, analysts and decision-makers can assess the risks associated with different events and make informed choices.

Moreover, the probability of disjoint events can be calculated using the formula P(A or B) = P(A) + P(B), where P represents the probability of an event. This formula makes it easier to determine the overall probability of events that are mutually exclusive.

Real-World Application

Disjoint events find application in various real-world scenarios, such as weather forecasting, sports predictions, and financial analysis. For instance, in weather forecasting, the probability of rain on a particular day and the probability of sunshine on the same day are disjoint events since they cannot occur simultaneously.

By analyzing the probability of disjoint events, meteorologists can provide accurate forecasts and help people make informed decisions based on the weather conditions. This application highlights the practical significance of understanding and computing the probability of disjoint events.

Understanding what disjoint events are is crucial in various fields due to its practical applications. In data analysis, it helps in identifying events that have no outcomes in common. For instance, in marketing analytics, knowing the disjoint events can assist in optimizing marketing strategies by targeting different consumer segments effectively.

Business Decision Making

Disjoint events play a vital role in business decision-making processes. By analyzing the probability of disjoint events occurring, businesses can make informed decisions to minimize risks and maximize opportunities. This statistical approach enhances forecasting accuracy.

Risk Management

When it comes to risk management, identifying disjoint events can help in assessing and mitigating potential risks. By understanding the probability of disparate events, risk managers can develop effective strategies to protect assets and investments.

As we conclude our exploration into the realm of disjoint events, it becomes evident that these seemingly mysterious occurrences can be dissected and understood through logical reasoning and probability concepts. By grasping the essence of what disjoint events entail – events that cannot happen simultaneously – you unlock the key to making informed decisions and predictions in various fields including statistics, economics, and even everyday life scenarios.

By recognizing the fundamental characteristics and implications of disjoint events, you are equipped to navigate uncertainties with more confidence and precision. Remember, mastering the concept of disjoint events empowers you to analyze situations with a clearer perspective, enhancing your problem-solving abilities and decision-making skills.

So, the next time you encounter disjoint events in your studies or professional endeavors, embrace the opportunity to unravel their mysteries and harness their potential to your advantage!